다이나믹 프로그래밍 = 동적 계획법
- 동적
자료구조 : 프로그램이 실행되는 도중 실행에 필요한 메모리 할당하는 기법
다이나믹 프로그래밍: 의미 없음
- 조건
1. 최적 부분 구조
: 큰 문제를 작은 문제로 나눌 수 있음, 작은 문제의 답을 모아 큰 문제 해결
2. 중복되는 부분 문제
: 동일한 작은 문제 반복적으로 해결
- 피보나치 수열
1,1,2,3,5,8,13,21,34,55,89
점화식 : 인점한 항들 사이의 관계식
수열을 배열/리스트에 저장
#피보나치 수열 끝날 때를 명시(x == 1 / x == 2)
def fibo(x):
if x == 1 or x == 2:
return 1
return fibo(x-1) + fibo(x-2)
print(fibo(4))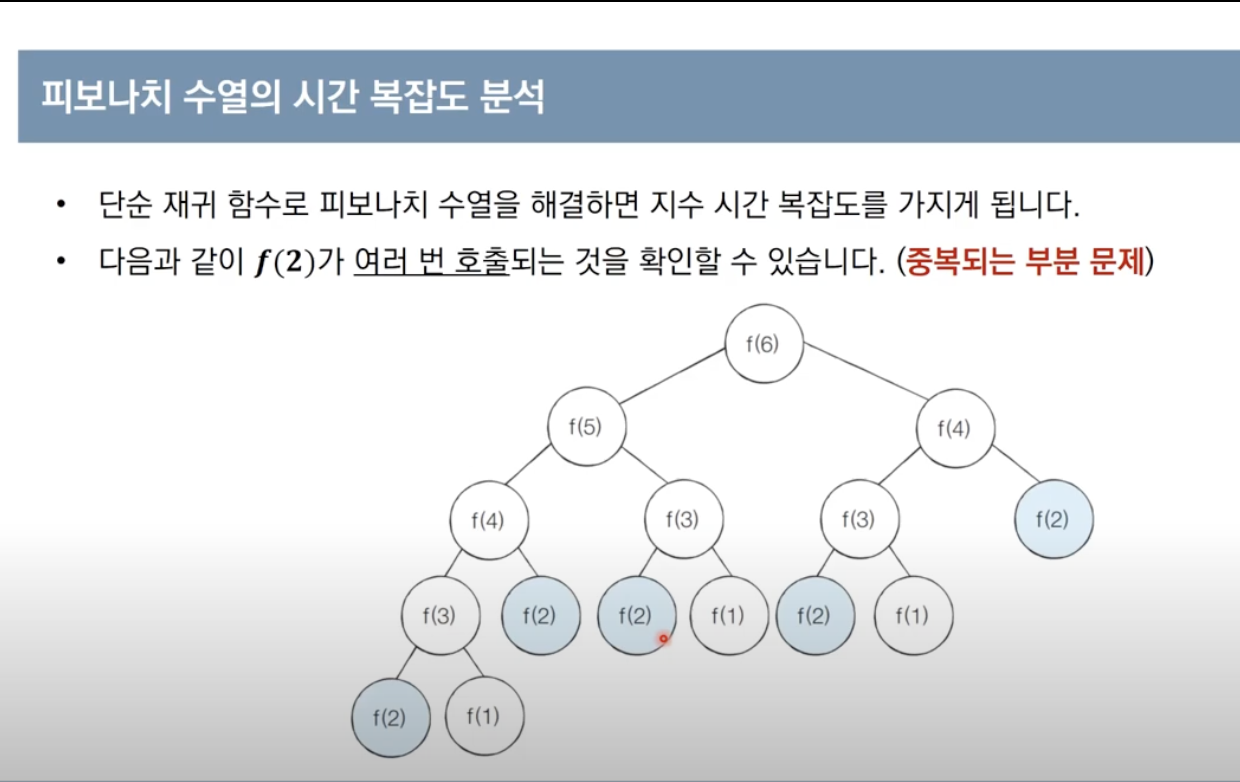
- 탑타운 = 하향식 = 메모이제이션
한 번 계산한 결과를 메모리 공간에 메모하는 기법 => 캐싱
다이나믹 프로그래밍을 위해 사용하지 않을 수도 있음
d = [0] * 100
def fibo(x):
#종료 조건 , x가 1 혹은 2일 때 1 반환
if x == 1 or x == 2:
return 1
# 이미 계산한 적 있는 문제면 그대로 반환
if d[x] != 0:
return d[x]
d[x] = fibo(x-1) + fibo(x-2)
return d[x]
print(fibo(99))
- 보텀업 = 상향식 (다이나믹 프로그래밍의 전형적인 형태)
결과 저장용 리스트 -> DP 테이블
- 다이나믹 프로그래밍 VS 분할정복 (퀵정렬)





n = int(input())
array = list(map(lnt, input().split()))
d = [0] * 100
#다이나믹 프로그래밍 진행(보텀업)
#첫번째 원소의 얻을 수 있는 최댓값은 첫번쨰 원소
d[0] = array[0]
d[1] = max(array[0], array[1])
for i in range(2,n):
d[i] = max(d[i-1], d[i-2] + array[i])
print(d[n-1])'Python > 이것이 취업을 위한 코딩테스트다' 카테고리의 다른 글
| [이코테] 다익스트라 알고리즘 (0) | 2025.03.11 |
|---|---|
| [이코테] 최단경로 알고리즘 (0) | 2025.03.10 |
| [이코테] 파라메트릭 서치 (0) | 2024.11.25 |
| [이코테] 이진탐색 (0) | 2024.11.23 |
| [이코테] 이진탐색 (0) | 2024.11.21 |